This article describes the use of LabVIEW software programming, using a data acquisition card with an optical power meter, through the blade cutting beam method to measure and calculate the beam waist radius of the femtosecond pulsed laser. By fitting the relationship between the optical power and the position of the blade, the laser beam waist radius with an accuracy of micron can be measured online in real time. The femtosecond laser beam waist radius near the focus of the condenser lens was measured. It is found that the change of the waist radius with the position before the focus satisfies the large radius of the Cambodian waist measured after the focus, which is mainly due to the great peak power of the femtosecond laser after focusing, which has a destructive effect on the blade.
1 Introduction
The invention of laser has a great impact on people's work and life. The research on the nature of quantum dot laser from the ruby ​​laser in 1960 to the end of the 21st century has always been a hot spot for scientists. The basic properties of a laser mainly refer to its frequency domain and time domain properties. In order to specify and discuss the propagation characteristics of a laser beam, its spot radius must be defined. The commonly adopted definition is the peak of the beam illuminating (the strongest), and the radius of the axial or numerical value is attenuated by 1/e2 (13.5%), which we call the beam waist radius of the laser. Usually, it is necessary to judge the spot size and position of the laser in real time to further optimize the experimental results. It is necessary to observe and calculate the size and position of the spot on the line. Based on this purpose, the blade method is used to measure the laser beam waist radius in real time. Calculation.
In optical experiments and practical applications using lasers, the beam waist radius of the laser is a very important physical quantity. For experiments such as Z-scan, fluorescence dynamics and laser micromachining, it is necessary to determine the beam waist radius of the laser. Its measurement accuracy directly affects the accuracy of experimental data and analysis. At present, the methods for measuring the spot size include a slit method, a Ronchi grating method, a Radon analysis method, a Talbot effect method, and a knife edge method. The knife-edge method uses a measuring method for measuring the transmitted light intensity. The flat edge of the cutting edge is used, and the transmittance function is a step function. When the photoelectric receiving element is as close as possible to the cutting edge, the diffraction amount is reduced, and the μm level is accurately measured. Spot size is feasible. The cross-sectional shape of the laser we usually touch in the TEM (transverse mode and longitudinal mode is 0) mode is Gaussian, which we call Gaussian beam.
2 Basic properties and measurement principle of Gaussian beam
The field strength distribution of the Gaussian beam along the z-axis cross section can be expressed as:
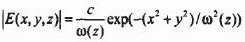
Where c is a constant factor, x, y is the coordinate in the cross section perpendicular to the z-axis of the beam direction, and ω(z) is the beam waist radius at z. The beam transmitted by the Gaussian beam passing through the lens is still a Gaussian beam. The beam waist radius of the beam varies with the coordinate z (beam propagation direction) in a hyperbolic law. At the image side, the spot is the smallest at the focal position of the lens. The intensity distribution in the cross section at the waist of the Gaussian laser beam can be expressed as:
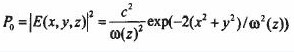
Where Po is the total power of the laser, ω(z) is the beam waist radius defined by the intensity 1/e2, and the Gaussian beam field is not limited to the beam waist radius, theoretically it extends laterally to infinity, only The light intensity is weaker in the area larger than the waist radius.
The optical power transmitted when the blade cuts the laser beam can be expressed as:
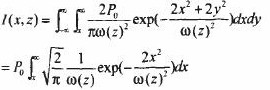
ω(z) is the beam waist radius at different positions defined by the intensity 1/e2, and the formula (3) can be reduced to:
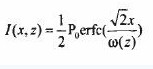
It can be seen that l(x,z) is a Guassian error function whose derivative to x is:
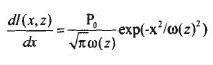
It can be seen that only the optical power transmitted by the blade when cutting the laser beam varies with the position of the blade, and then the derivative of the Gauss is used to obtain the beam waist radius at the corresponding position.
Mgo Board,Magnesium Oxide Building Board,Magnesium Oxide Backer Board,Magnesium Oxide Board
Shangdong Oushibao New Materials Co.,Ltd , https://www.oushibaomgo.com